Un nouveau modèle pour le tenseur de dilatation.

On a commencé par utiliser un modèle simple pour le tenseur de dilatation. Malheureusement notre modèle simple qui suffit lors de la phase de pressage, où la temprérature est croissante où constante, n'est plus suffisant lors du refroidissement, ou si on tient compte de fluctuations de la température lors du pressage. On va donc s'attarder à dévelloper un modèle pour ce tenseur.

Index de polymérisation et tenseur de dilatation.

On cherche à définir la contribution de la composante thermique aux déplacements. On observe d'abord que l'effet est essentiellement dans le plan, et qu'il s'agit d'une contraction. Dans une première approche on tient compte de cette contribution via un terme source linéaire par rapport à la température:
FV(t,T) = -div(EßT(T-T0)).
Par la suite on peut enrichir le modèle en considérant que ßT dépendant de façon plus ou moins complexe du temps et des autres paramètres du problème. Résumons grossièrement les propriétés que l'on attend de la dilatation:
  1. Pas de dilatation en dessous d'une température critique (FV est nulle ou constant en dessous d'une température critique).
  2. La dilatation est irréversible (FV est croissante par rapport au temps: FV(tn+1) >= FV(tn)).
  3. Au dessus de la température critique, la dilatation ne s'arrêtera pas même si  on note une diminution de la température (FV est constante si la température est en dessous de la température critique. La croissance ne dépend pas de la température mais la vitesse en dépend).
  4. Une fois la dilatation maximale atteinte le processus s'arrête (FV devient constant une fois la dilatation maximale atteinte).
Les propriétés 2 à 4 rendent l'emploi d'un terme linéaire (par rapport à la température) pour la contribution thermique aux déplacements très difficile. Pour respecter ces propriétés il faudra définir un tenseur ßT dépendant de la température et du temps de façon fort complexe. Plutôt que d'envisager des termes compliqués pout les composantes de  ßT on va utiliser un terme qui ne dépend pas linéairement de la température pour FV.

Les propriétés présentées plus haut ressemblent à celles que l'on exigerait de la polymérisation. Il est clair que la contraction des papiers (de finition et de contre-balancement),  que l'on associe à la chaleur dans le système, est aussi liée à la polymérisation. Pour simplifier l'expression du tenseur de dilatation thermique et définir FV on va s'inspirer du comportement de la polymérisation.

index F
Illustration des 4 propriétés exigées: pas de polymérisation sous la température critique, une fois cette
température atteinte la polymérisation reste croissante ou constante (quand la température redescend
sous la température critique) et pour finir F est constant une fois la valeur maximale (F =1.) atteinte.

D'abord on introduit l'index de polymérisation F(t,T) ( Kiran E., R. Iyer. 1994. "Cure behavior of paper-phenolic composite systems: kinetic modeling." J. Applied Polymer Science 51:353-364.). Cette index est en fait un indicateur de l'ampleur de la polymérisation et il satisfait l'équation:

dF/ dt = A e -E/RT (1-F)p       F(0) = 0.

A = constante de réaction  (1/s)                           T = température en K
E = énergie d'activation de la  réaction (J/mol)         p = ordre de la réaction
R = constante des gaz (8.31696 J/mol/K)

Les paramètres A,E et p dépendent  de la résine dont sont imprégné les papiers et ils sont habituellement déterminés expérimentalement. Pour vérifier la propriété 1, on modifiera l'équation de F en utilisant 
A(T) = A*H(T>TCr) 
H(T>TCr) = 1 si T >=TCr ,  H(T>TCr) = 0 si T <TCr   

Alors si T <TCr   sur l'intervalle (ta,tb) on a dF/dt = 0 sur (ta,tb) et  F = F(ta) sur (ta,tb). Il faut noter que F ainsi défini satisfait les propriétés 1-4 et que 0 <= F <= 1.

On défini la force volumique FV responsable des dilatations thermique comme la divergence du produit tensoriel de E (le tenseur d'élasticité) et de ßT :
FV = -div(E:ßT )
ou le tenseur de dilatation est défini comme
ßT(t,T) = F(t,T)*ßExp(t)
où ßExp est un tenseur d'ordre 2 dépendant des résultats expérimentaux portant sur la dilatation.

Détermination de ßT(t,T).

Pour caractériser complètement le tenseur ßT il nous reste à
  1. Déterminer comment on calcul l'index de polymérisation.
  2. Déterminer le tenseur ßExp(t) en fonction des valeurs expérimentales obtenues pour la dilatation des deux types de papier.

    1. Calcul de l'index de polymérisation F.

L'index est construit à partir de trois paramètres: p l'ordre de la réaction et E l'énergie de réaction qui dépendent de la nature de la résine et que l'on supposera constants; A la constante de réaction qui nous servira à calibré l'index en fonction du temps imposé pour une polymérisation totale.

Les valeurs retenues correspondent à une résine utilisée lors de la fabrication d'OSB (Ahmad, M. 2000. "Cure Characteristics of Phenol Formaldehyde Resin." Unpublished Report. Dept. of Wood Science and Forest Products, VPI & SU, Blacksburg, Virginia et Stenberg N. ,"Mechanical properties in the thickness direction of paper and paperboard"  thèse à Department of Solid Mechanics, Royal Institute of Technology Stockholm, Suède.) :

E = 12423.0
p = 0.587

On suppose que la polymérisation est complète lors de l'ouverture des presses, après TPr = 20 secondes, c'est en variant A que l'on y arrivera.

Remarque: Il est tout à fait possible que les valeurs retenues ne soient pas valides pour les matériaux que l'on considèrent. Dans ce cas F ne représentera pas l'index de polymérisation de la résine employée lors de la fabrication. Cependant F satisfera les propriétés 1 à 4 et la dilatation ainsi définie aura des propriétés physiques plus près de la réalité. Pour nous l'important n'est pas d'avoir une représentation exacte de la polymérisation mais plutôt d'avoir pour la dilatation un comportement mécanique réaliste.

Il nous reste un paramètre à fixer pour déterminer complètement F, c'est A la constante de réaction. Nous ne prenons pas la valeur proposée dans Stenberg ("Mechanical properties in the thickness direction of paper and paperboard"  thèse à Department of Solid Mechanics, Royal Institute of Technology Stockholm, Suède.)
car cette valeur ne satisfait pas les temps de polymérisation auxquels on s'attend (ce qui est normal puisqu'il s'agit des paramètres associés à un autre problème et à d'autres matériaux). On va plutôt calibrer A pour avoir une polymérisation à 100 % à 20 secondes. On suppose aussi que la polymérisation n'est pas complète mais relativement avancée après 10 secondes. On va imposé arbitrairement que la polymérisation soit d'environ 85% à 10 secondes.

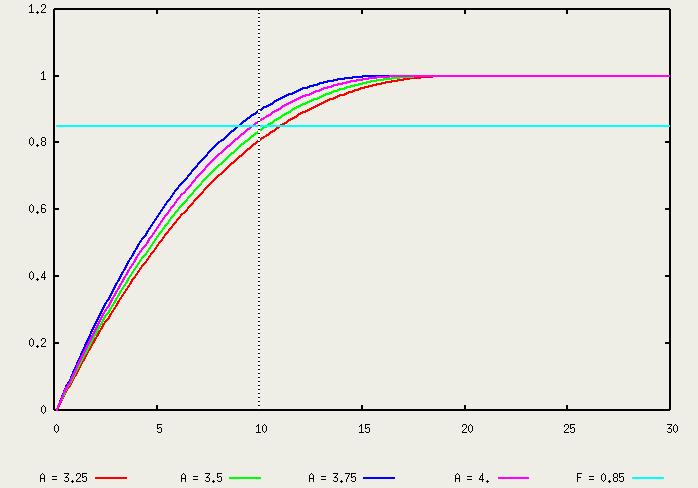effet de A sur F
Graphiques de différentes valeurs de F pour une variation de la constante de réaction pour une
température fixé à 180 C pendant 30 secondes.

L'équation différentielle ordinaire de F peut se résoudre facilement.  On va employé pour appoximer la solution la méthode d'Euler explicite:

h = tn - tn-1         F(tn) = Fn = Fn-1 + h A e -E/RT(tn-1) (1-Fn-1)p      F0 = 0       n = 1,...,N

En comparant la solution avec cette méthode et la méthode d'Euler implicite nous  estimons que le schéma est stable et la valeur retenue pour la constante de réaction est
A = 3.5

Le schéma retenu a deux avantages importants: il est simple d'emploi puisque la solution pour un pas de temps donné s'obtient par l'évaluation d'une expression explicite; en second lieu, mais cela découle du premier avantage, l'ajout de F dans le système d'équation à résoudre est transparent car il se fait au niveau du fichier champs.

    2. Calibrage du tenseur ßExp(t)

Il nous faut d'abord résourdre le problème de la définition des coefficients d'élasticité. Ces coefficients sont tirés des résultats expérimentaux. Nous allons présenter maintenant comment nous avons utilisé ces résultats.

ATTENTION. Avec la présence du papier il nous faut aussi introduire un repère puisque les propriétés ne sont plus isotropes. Plus précisément il nous faut définir le sens machine MD et sa perpendiculaire CD. On a fixé pour la suite le sens machine comme étant parallèle à l'axe des Y et la direction CD parallèle à l'axe des X.   

    2.1. Elasticité


Commneçons par le papier de contre-balancement qui est le plus facile à traiter. Les valeurs de module d'Young obtenues sont


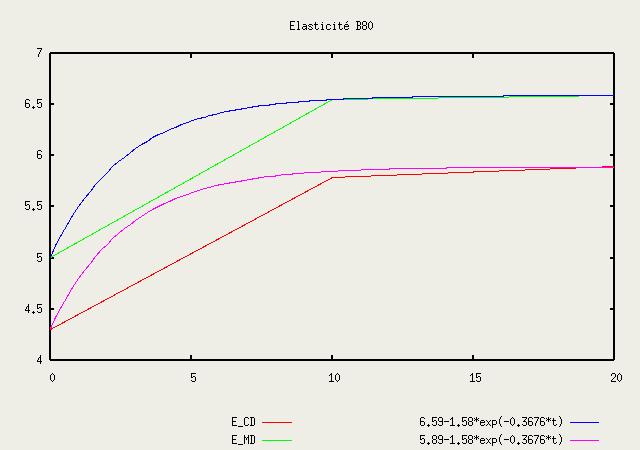
 X (GPa)
 Y (Gpa)
0 sec
 4.299
 5.010
10 sec
 5.788
 6.550
20 sec
 5.892
 6.589

Ces valeurs nous suggérent un comportement exponentielle pour  le module dans chaque direction:

elasticite kraft

ECD = EX = 5.89 - 1.58 e -0.3676 t 
EMD = EY  = 6.59 - 1.58 e -0.3676 t = EX  + 0.7

Les données présentées pour les papier de finition et d'overlay sont plus difficiles à interpréter. Voici les résultats ainsi que deux tableaux supplémentaires


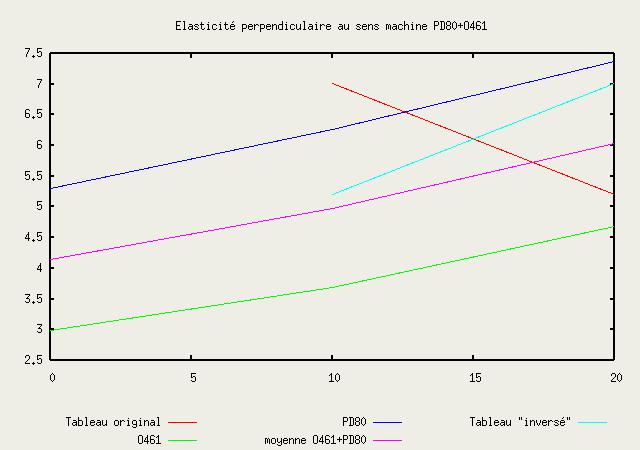
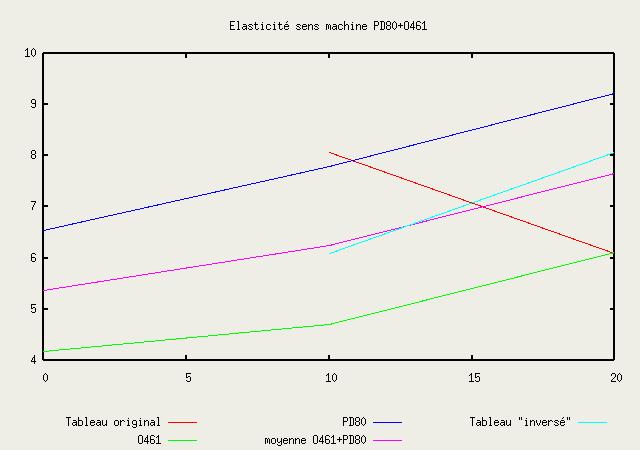
 PD80 (GPa)
 O461 (GPa)
 PD80+O461 (GPa)
 PD80+O461 Inversé
 Moyenne  des modules
X
 Y
 X
 Y
 X
 Y
 X
 Y
 X
 Y
0 sec
 5.296
 6.535
 2.982
 4.182
 N/A
 N/A
 N/A
 N/A
 4.139
 5.35585
10 sec
 6.257
 7.790
 3.687
 4.696
 7.006
 8.075
 5.208
 6.088
 4.972
 6.243
20 sec
 7.374
 9.219
 4.687
 6.105
 5.208
 6.088
 7.006
 8.075
 6.0305
 7.662

Le fait que le module d'Young soit plus petit après 20 secondes de "cuisson" me semblant bizarre j'ai donc inversé les valeurs pour 10 et 20 sec. J'ai ensuite fait une simple moyenne arithmétique des valeurs de modules observés pour les deux papiers. Les "modules d'Young moyens" se comportent comme les modules du tableau inversé ce qui me semble raisonnable.

PD80+O461 direction CD

PD80+O461 direction MD

On va  se servir des valeurs moyennes pour les valeurs de module à 0 sec. Utilisant comme pour le papier de contre-balancement une exponentielle on a:

ECD = EX = 2.5715 + 1.5676 e 0.052 t 
EMD = EY  = 4.9353 + 0.4232 e 0.1002 t


elo


Remarque: Si j'ai erré et le tableau originale doit être considéré il nous faudra alors refaire les calculs dans ce qui suit. De plus il serait alors important d'avoir des valeurs pour des temps intermédiaires. Rappelons qu'un module d'Young qui diminue correspond à des déplacements qui augmente et vice-versa (toute chose étant égale par ailleurs). Ainsi le papier serait plus "mou" après 20 secondes  comparativement  au même  papier après  10 secondes.

2.2. Les valeurs expérimentales.

Nous avons comme valeurs:


 PD80 + O461 B80
temps 10 sec 20 sec 10 sec 20 sec
MD 0.71% (0.00866 m) 0.99%  (0.01207 m) 0.76% (0.00927 m) 0.84% (0.01024 m)
CD 0.99% (0.00604 m) 0.93%  (0.00567 m) 0.96% (0.00585 m) 1.22% (0.00744 m)

J'ai mis entre parenthèses les valeurs absolues de contraction sur deux des côtés (par symétrie on a la même contraction sur le coté opposé) d'un panneau  de  4' x  8'  (1.219202 m X 2.438404 m).


Largeur (X) (m)
 Longueur (Y) (m)
 Epaisseur (Z) (m)
PD80+O461
 0.609601
 1.219202
 0.00034
MDF
 0.609601 1.219202 0.007
B80
 0.609601 1.219202 0.00034

Pour calibrer le tenseur on essaie de reproduire numériquement le test qui est utilisé pour obtenir les résultats du tableau précédent. J'ai exploité pour cela le plus possible les résultats de labo.


 PD80+O461
 B80
 MDF
densité:rho
  940 kg/m3  (0)
 730 kg/m3  (1)
 800 kg/m3
Équation en T

CT  -> J/(Kg C)
KT -> J/(m sec C) 		CT=1.2 CTMDF          (4)
KT= KTMDF-0.008       (4)
 CT=1.2 CTMDF          (4)
KT= KTMDF-0.008       (4)

 CTMDF=1000*(0.1031+0.003867(T+273.15)+0.042M)/(1+0.01M)  (2)
KT = KTMDF=(rho/1000)*(0.217+0.0038M)+0.024                           (3)

Équation en M

CM -> %-1

KM -> Kg/(m sec %)




            voir MDF     -->



  
         voir MDF  -->
  CM=0.01
 [KM]x = [KM]y= 0  [KM]z = KMMDF avec

KMMDF= KM0
 M <= 6.6
KMMDF= KM0 + (KM1-KM0)*(M-6.6)/(9-6.6)
 6.6 <= M <= 9
KMMDF= KM1
 M <= 9
 KTM = 0.1*KM

 KM0 = 8.0e-10 KM1= 8.0e-11                          (5)
Équation en U
E -> Pa
BM-> %-1
(6)

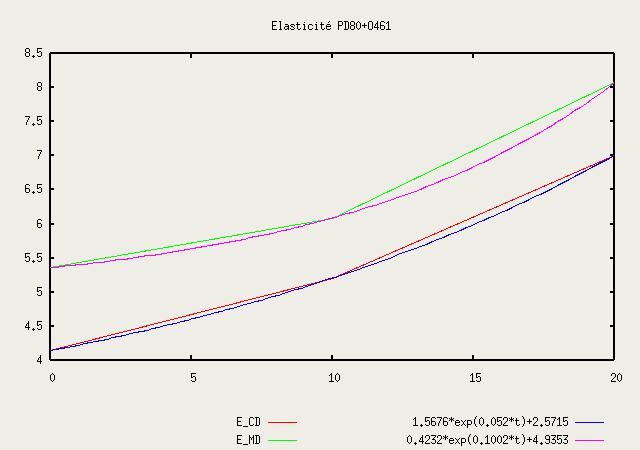
EX = 1e9(2.5715 + 1.5676 e 0.052 t)

EY  = 1e9(4.9353 + 0.4232 e 0.1002 t)

Ez = 0.01 EMD    (7)

ßM = ßMMDF --->
(6)
EMD = 1e9(6.59 -1.58 e-0.3676t)
ECD = EMD -  0.7e9            
Ez = 0.01 EMD                 (7)



ßM = ßMMDF --->

 [EMDF]x = [EMDF]y  = E1   [EMDF]z = E3 avec pour i=1 et 3

Ei= Ei0
 M <= 6.6
Ei= Ei0 + (Ei1-Ei0)*(M-6.6)/(9-6.6)
 6.6 <= M <= 9
Ei= Ei1
 M <= 9

 E10 = 2.2e9, E11 = 1.9e9, E30 = 6.1e7, E31 = 4.4e7    (5)

[ßM]x = [ßM]y = ß1    [ßM]z = ß3  avec pour i = 1 et 3

ßi  = BMi0        dM/dt >= 0
ßi  = BMi1        dM/dt < 0
BM10 = 3.6e-4, BM11 = 7.7e-4, BM30 = 8.4e-3, BM31 = 9.5e-3 (5)

[ßT]x = [ßT]y =  [ßT]z = 0 

 



Cond. Initiales
 Cond. Limites 0 <= t <= 21
 Cond. Limites 21 <  t
T  (C)
 T0 = 20
   T = TPr  sur \[ \Gamma_h \] et \[ \Gamma_b \]   TPr = 180 
  qT = hT(T-Ta)  sur \[ \Gamma_h \], \[ \Gamma_b \] et sur la rive
 Ta = 20, hT = -5.                                             (8)
M (%)
 M0 = 10   qM= hM(M-Ma)    sur la rive   Ma = 10  qM= hM(M-Ma)   sur \[ \Gamma_h \], \[ \Gamma_b \] et sur la rive 
 Ma = 10 hM = -3.2e-5                                     (5)
U (m)
U0 = (0,0,0)     s0 = 0 (tensoriel)   \[ \sigma_n = P \]  = P*n sur \[ \Gamma_h \]    Uz = 0 sur \[ \Gamma_b \]
 P = 3.5e6 t
0<= t <= 1
 P= 3.5e6
 1 <= M <= 20
 P= 3.5e6 (21-t)
 20<= t <= 21
+ conditions de symétrie
  Uz >= 0 sur \[ \Gamma_b \]
+ conditions de symétrie


(0) Moyenne  grammage/épaisseur pour PD80 et O461 rapport du 31 déc. (0.19 mm et 0.15 mm respectivement).
(1) Grammage/épaisseur rapport du 31 déc. (0.35 mm)
(2) Cette définition vient du chapitre 3 de "Forest Products Laboratory." 1999. Wood handbook--Wood as an engineering material. Gen. Tech. Rep. FPL-GTR-113. Madison, WI: U.S. Department of Agriculture, Forest Service, Forest Products Laboratory. 463 p.  http://www.fpl.fs.fed.us/documnts/fplgtr/fplgtr113/fplgtr113.htm
(3) e-mail de l'an passé.
(4) On fait l'hypothèse que la chaleur spécifique du papier est supérieure à celle du MDF mais que la diffusion elle est inférieure (mais toujours linéaire par rapport à M).
(5) valeurs obtenues par Ganev pour le MDF (article no. 4, table 2).
(6) Interpolation construite à partir des valeurs du rapport du 31 déc. pour le MOE
(7) Basé sur "Mechanical properties in the thickness direction of paper and paperboard" Niclas Stenberg, thèse à Department of Solid Mechanics, Royal Institute of Technology Stockholm, Suède: http://www.fpirc.kth.se/Download/Niclas_Stenberg_99.pdf
(8) "Inspiré" de "Experimental Determination of Convective Heat and Mass Transfer Coefficients During Wood Drying" M. Nabhani, C. Tremblay et Y. Fortin, 8th International IUFRO Wood Drying Conference - 2003

REMARQUE: On ne s'interesse qu'a avoir des paramètres dont les ordres de grandeurs soient réalistes. La précision n'est pas ce qu'on recherche.

Essais avec valeurs constantes/non-constantes.

J'ai fait le calcul  avec les valeurs présentées au tableau  en utilisant des valeurs constantes pour tout les coefficients. Pour les valeurs constantes j'ai fixe T à 100 et M à 10 dans les calculs de CTMDF et KTMDF .

Il s'agit, avec les valeurs du tableau précédent, de déterminer les valeurs du tenseur ßT . On suppose que le tenseur n'a pas de composante dans l'épaisseur et qu'il se ramène à une paire de composantes dans le plan XY, soit ßX et  ßY. Pour obtenir la valeurs de ces composantes on part des valeurs relatives de contraction obtenues en laboratoire  pour 0, 10 et 20 secondes. On suppose pour le moment que le tenseur est constant:


ßExp(t) = ßExp=

ßX 0
 0
0
 ßY 0
0
 0
 0

Dans ce cas nous ne pourrons pas faire coincider exactement les valeurs numériques de contractions avec les mesures expérimentales. Néanmoins, répétons le encore une fois, nous aurons des valeurs relativement réalistes dont nous nous contenterons pour l'instant. On va s'assurer que la valeur numérique de la contraction obtenues à 20 secondes corresponde avec la valeur expérimentale. Notons que les valeurs du tenseurs ont été obtenues par tatonnements.


 PD80+O461 B80
ßX -0.0099039105
 -0.0122016
ßY -0.009896541
 -0.0083961

Il est interessant de comparer ces résultats avec le tableau des valeurs relatives de contractions après 20 secondes:


 PD80+O461 B80
CD 0.93%
1.22%
MD 0.99% 0.84%

Si on tient compte des erreurs produites par l'approximation numérique il est clair que les composantes du tenseur correspondent aux valeurs du tableau des contractions. On a attribué à des erreurs expériementales la différence entre la contraction à 10 et 20 secondes dans le cas du papier de finition (le tableau indique que le papier est en extension) et on a pris dans ce cas la valeur de 99% après 20 seconde. Dans tout les cas on voit qu'il n'y a pas correspondance à 10 secondes entre le numérique et l'expérimentale, ce qui était prévisible, la contraction ne pouvant être totalement attribuée à la polymérisation.

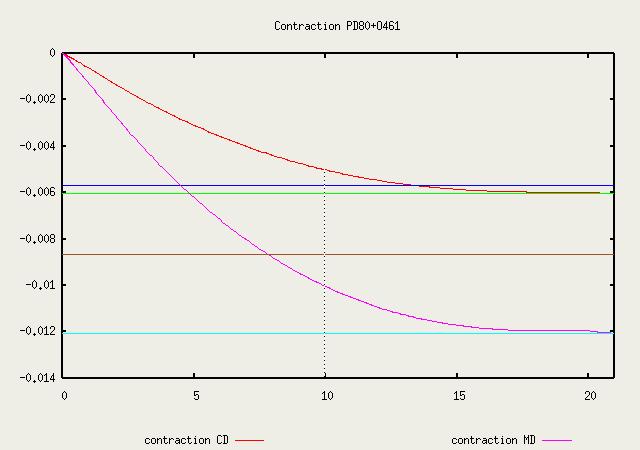contraction pour papier finition
contraction dans les direction MD (déplacement UY) et CD (déplacement UX) pour le papier finition


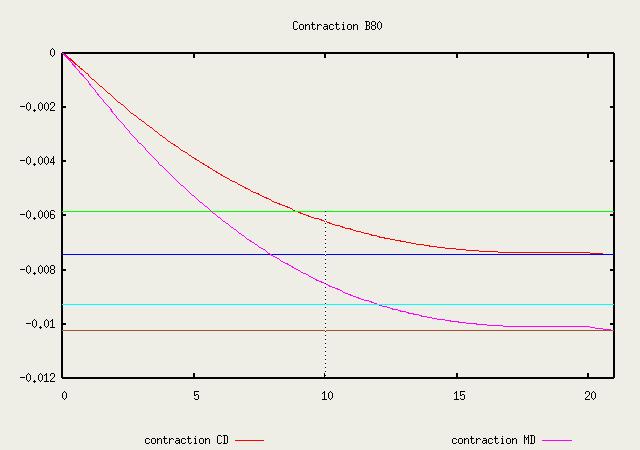contraction pour B80
contraction dans les direction MD (déplacement UY) et CD (déplacement UX) pour le papier contre-balancement B80.