L’équipe du GIREF et des collègues de Michelin ont participé en juin dernier à l’événement « Calculs à l’échelle » organisé par SciNet et se déroulant sur le super-calculateur Niagara. L’objectif visé était de tester encore plus loin la capacité de MEF++ à résoudre des problèmes de grandes tailles. La dernière limite atteinte était de 4.6 milliards d’inconnues. Cette fois, les gens de SciNet nous offraient la possibilité d’utiliser 1946 noeuds Skylake/Cascade Lake, soit la totalité des noeuds disponibles de Niagara pour tenter un calcul.
Nous avons donc généré un maillage assez imposant pour occuper tous les noeuds, soit un cube dont chaque côté est divisé 2304 fois que nous avons obtenus en lançant la division en 2 de toutes les arêtes du cube divisé 1152 fois qui avait précédemment été utilisé en 2019 pour le calcul à 4.6 milliards d’inconnues. Nous avons fait ce travail de division de maillage sur 180 processus et obtenu le nouveau cube en 5345 secondes, dont 4033s pour l’écriture du fichier de près de 5 téraoctets, ce qui donne:
| Type de composante | Quantité |
| Sommets | 12 246 522 625 |
| Arêtes | 36 723 628 800 |
| Faces | 36 707 696 640 |
| Hexaèdres | 12 230 590 464 |
La physique du calcul à faire était la même qu’en 2019, soit un calcul en grandes déformations hyper-élastiques. Nous avions depuis optimisés les termes de formulation de Nitsche utilisés pour l’imposition des conditions de Dirichlet. En plus de lancer à plusieurs répétitions le calculs à 4.6 milliards d’inconnues avec différents nombres de processus, nous avons pu lancer le calcul sur le nouveau maillage totalisant 36.7 milliards d’inconnues en utilisant 31 136 processus.
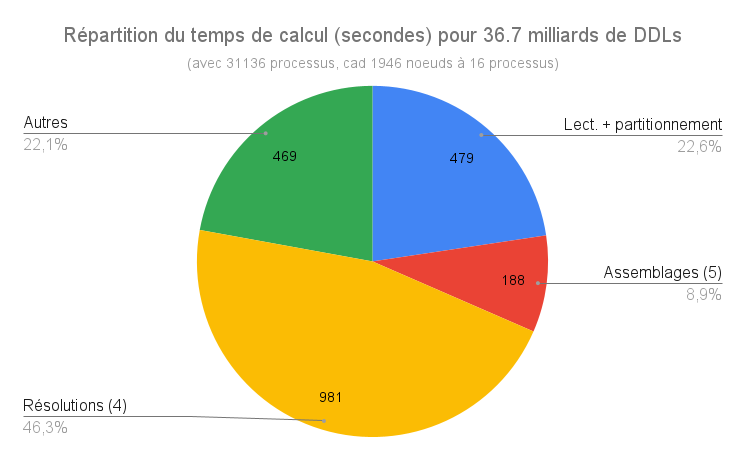
Après quelques soucis avec les sorties écran (inutile de récupérer 32k fichiers de sorties écran…) le calcul a bien démarré et 4 itérations de Newton ont été faites en utilisant un solveur FGMRES et le préconditionneur GAMG de PETSc 3.17.2 (détails complets). La dernière itération de Newton a donnée une correction telle que le calcul allait diverger: en effet, le déplacement imposé en Z de 0.05 était trop grand pour cette taille de maille car il y a 115 couches d’éléments dans une hauteur de 0.05! La prochaine fois, il suffira d’imposer le déplacement en 2 étapes. Le calcul a dû être arrêté pendant la 5e itération et faute de temps, n’a pu être relancé… Voici malgré tout, la répartition du temps de calcul utilisé:
Il est à noter que chaque phase d’assemblage a pris environ 37s, soit exactement le même temps que pour le calcul à 4.6 milliards de DDLs sur 4096 processus, soit une charge équivalente par processus! Le temps de lecture du maillage donne une vitesse de 10.6 Go/s, ce qui intéressant mais pourrait encore être amélioré.
Malgré la divergence du Newton, nous sommes fiers d’avoir pu lancer un tel calcul qui nous a permis d’identifier plusieurs portions de code à améliorer. Nos avancées devraient avoir des retombées sur tous les calculs parallèles que nous et notre partenaire Michelin faisons.
Nous tenons à remercier chaleureusement l’équipe de SciNet, en particulier Ramses va Zon et Erik Spence pour leur précieuse aide tant à la préparation de ces calculs que lors du lancement lui-même. Nous serons prêts pour le prochain événement « calculs à l’échelle » pour faire converger ce calcul!

Bonjour,
Wow, 36 milliards d’inconnues! C’est pas de la petite bière! Félicitations! 🙂
Je serais bien curieux de voir comment MEF++ a évolué durant les 15 dernières années (architecture, évolution du C++, algorithmie, performances, etc). En tous les cas, je suis bien content de voir que le code est toujours utilisé et contribue à la recherche au GIREF.
En espérant que tout le monde se porte bien et que l’avenir du groupe soit prometteur.
À la prochaine.
Carl