Gauchissement hydrique des composites à base de bois
Il s'agit ici de produire un code utilisant MEF++ pour reproduire les résultats obtenus par S. Ganev à l'aide de ABACUS (Finite Element Modeling of the Hygroscopic Warping of Medium Density Fiberboard, Wood Fiber Sci. 37, No 2, 337-354). Notons qu'une partie des résultats numériques sont validés par des résultats en laboratoire.
Le problème se résume de la façon suivante: développer un modèle éléments finis 3D pour l'étude des déformations hygro-mécaniques d'un panneau de MDF, avec différents profils de densité, causées par l'absorption d'humidité sur une seule face.
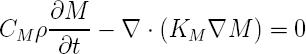
Pour les déplacements U, en petites perturbations, le tenseur des déformations s'écrit
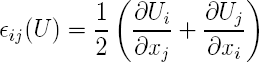
La loi de comportement, c'est-à-dire la relation entre le tenseur des déformations et le tenseurs des contraintes étant une loi de Hooke avec un couplage hydrique (on utilise la convention des indices répétés)
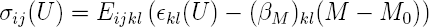
et finalement puisque l'on à pas de charge volumique externe et que l'on suppose un phénomène quasi-statique l'équation pour les déplacements est
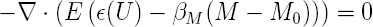
Sachant que le MDF est isotrope transverse nous connaissons la forme du tenseur des coefficients d'élasticité E. Dans notre cas l'axe d'isotropie sera la direction perpendiculaire au plan définissant le panneau et on aura un matériau qui sera isotrope dans le plan. On pourra définir le tenseur d'élasticité E à l'aide de 5 paramètres soit:
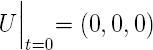
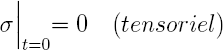
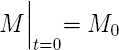
On suppose que toutes les faces du panneau sont imperméabilisées (flux nul) sauf une, la face supérieure. Pour la teneur en humidité on aura une condition d'échange (convection) avec l'humidité ambiante de la chambre:
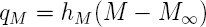 sur la face supérieure
sur la face supérieure
Pour les déplacements nous aurons des conditions de symétrie provenant de la nature des matériaux considérés et de la géométrie des panneaux. Ces symétries permettent d'étudier le quart du panneaux, ce qui réduit de façon importante la taille des maillages. Mais il s'agit d'un artifice numérique qui n'influence pas le comportement du panneau.
Nous sommes ici en présence d'un cas mentionné dans la rubrique portant sur les problèmes de contact. Nous observons les déformations d'un panneau sous l'effet de variation de la teneur en humidité. Hormis les conditions de symétrie la seule condition à appliquée se décrit comme suit: les déformations du panneau ne peuvent faire en sorte de déformer le support sur lequel le panneau est posée: pas de pénétration du panneau dans le support. Supposant que le support en question est un plan horizontal qui détermine l'origine de l'axe des z on aura comme condition au bords mécanique
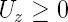 sur la face inférieure
sur la face inférieure
Avec cette condition notre problème devient un problème de contact. Il est clair que pour résoudre de tels problèmes le traitement habituel est innaproprié. En fait on utilisera une méthode de gradient conjugué projeté pour résoudre le problème d'optimisation sousjacent au problème de contact.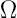 le panneau de MDF,
le panneau de MDF, 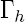 la face supérieure,
la face supérieure, 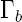 la face inférieure,
la face inférieure, 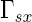 la face supportant la symétrie par rapport à l'axe des x,
la face supportant la symétrie par rapport à l'axe des x, 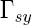 la face supportant la symétrie par rapport à l'axe des y. Ce qui fait en sorte que l'origine du repère corresponde avec le centre de la face inférieure du panneau
la face supportant la symétrie par rapport à l'axe des y. Ce qui fait en sorte que l'origine du repère corresponde avec le centre de la face inférieure du panneau
Le modèle pour la déformation d'un panneau de composite à base de bois se résume à la résolution du système d'ÉDP
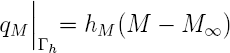
En plus du traitement particulier exigé par la condition de contact nous avons un problème lié aux conditions limites mécanique. Nous "manquons" de conditions aux bords, le problème est "mal posé" (au sens de Hadamard) puisque nous n'avons pas unicité de la solution. Le problème tel que proposé admet comme solution des translations dans une direction privilégiée d'une solution initiale (mouvements de corps rigide). Pour remédier à cette situation nous introduirons une modification à l'algorithme de résolution permettant d'exclure les mouvements de corps rigide. Notons que cette modification correspond à imposé qu'en tout temps au moins un point de la surface inférieure du panneau ait un déplacement nul. Ce qui correspond en fait à une condition limite du type:
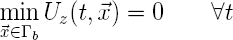
Pour finir voici un tableau des dimensions utilisé pour les différents coefficients et paramètres du problème.
Le problème se résume de la façon suivante: développer un modèle éléments finis 3D pour l'étude des déformations hygro-mécaniques d'un panneau de MDF, avec différents profils de densité, causées par l'absorption d'humidité sur une seule face.
Équations conservation
Le modèle physique est basé sur des équations de conservations et un certains nombre d'hypothèses permettant de préciser les équations régissant le phénomène à l'étude:- Équation de diffusion pour l'humidité (en 3D et instationnaire).
- Équation quasi-statique (la composante inertielle est négligée) de l'élasticité linéaire (l'hypothèse des petites perturbations est retenue).
- Puisque le modèle élastique est linéaire le matériau suit une loi de Hooke ce qui donne la forme de la relation entre les dilatations et l'humidité. De plus le MDF est supposé orthotrope; plus précisément isotrope transverse. Un matériau est dit isotrope transverse pour une propriété donnée si cette propriété est invariante par changement de direction obtenue par rotation autour d'un axe privilégié (axe d'isotropie).
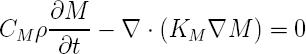
Pour les déplacements U, en petites perturbations, le tenseur des déformations s'écrit
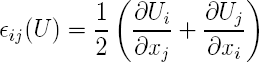
La loi de comportement, c'est-à-dire la relation entre le tenseur des déformations et le tenseurs des contraintes étant une loi de Hooke avec un couplage hydrique (on utilise la convention des indices répétés)
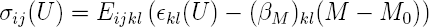
et finalement puisque l'on à pas de charge volumique externe et que l'on suppose un phénomène quasi-statique l'équation pour les déplacements est
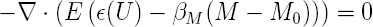
Sachant que le MDF est isotrope transverse nous connaissons la forme du tenseur des coefficients d'élasticité E. Dans notre cas l'axe d'isotropie sera la direction perpendiculaire au plan définissant le panneau et on aura un matériau qui sera isotrope dans le plan. On pourra définir le tenseur d'élasticité E à l'aide de 5 paramètres soit:
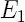 le module d'Young et
le module d'Young et 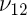 le coefficient de Poisson dans le plan.
le coefficient de Poisson dans le plan.
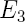 le module d'Young,
le module d'Young, 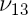 le coefficient de Poisson et
le coefficient de Poisson et 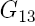 le coefficient de cisaillement dans la direction perpendiculaire au plan.
le coefficient de cisaillement dans la direction perpendiculaire au plan.
Conditions limites et initiales
Le modèle n'est pas complet sans la donné des condtions initiales des variables d'états M et U et les conditions limites qui leurs sont appliquées. Au début du processus on suppose que les panneaux sont à l'équilibre avec une teneur en humidité connue: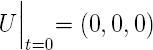
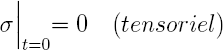
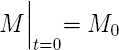
On suppose que toutes les faces du panneau sont imperméabilisées (flux nul) sauf une, la face supérieure. Pour la teneur en humidité on aura une condition d'échange (convection) avec l'humidité ambiante de la chambre:
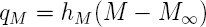 sur la face supérieure
sur la face supérieurePour les déplacements nous aurons des conditions de symétrie provenant de la nature des matériaux considérés et de la géométrie des panneaux. Ces symétries permettent d'étudier le quart du panneaux, ce qui réduit de façon importante la taille des maillages. Mais il s'agit d'un artifice numérique qui n'influence pas le comportement du panneau.
Nous sommes ici en présence d'un cas mentionné dans la rubrique portant sur les problèmes de contact. Nous observons les déformations d'un panneau sous l'effet de variation de la teneur en humidité. Hormis les conditions de symétrie la seule condition à appliquée se décrit comme suit: les déformations du panneau ne peuvent faire en sorte de déformer le support sur lequel le panneau est posée: pas de pénétration du panneau dans le support. Supposant que le support en question est un plan horizontal qui détermine l'origine de l'axe des z on aura comme condition au bords mécanique
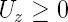 sur la face inférieure
sur la face inférieureAvec cette condition notre problème devient un problème de contact. Il est clair que pour résoudre de tels problèmes le traitement habituel est innaproprié. En fait on utilisera une méthode de gradient conjugué projeté pour résoudre le problème d'optimisation sousjacent au problème de contact.
Le modèle
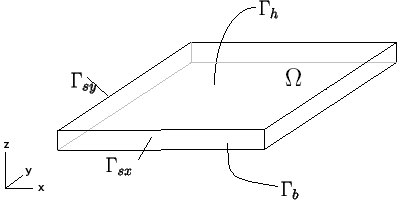
Soit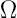 le panneau de MDF,
le panneau de MDF, 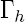 la face supérieure,
la face supérieure, 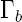 la face inférieure,
la face inférieure, 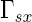 la face supportant la symétrie par rapport à l'axe des x,
la face supportant la symétrie par rapport à l'axe des x, 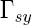 la face supportant la symétrie par rapport à l'axe des y. Ce qui fait en sorte que l'origine du repère corresponde avec le centre de la face inférieure du panneau
la face supportant la symétrie par rapport à l'axe des y. Ce qui fait en sorte que l'origine du repère corresponde avec le centre de la face inférieure du panneau
Le modèle pour la déformation d'un panneau de composite à base de bois se résume à la résolution du système d'ÉDP
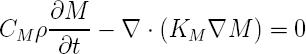 | dans 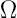 |
||
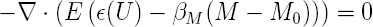 | |||
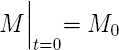 |
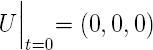 |
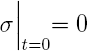 |
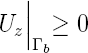 |
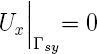 |
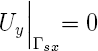 |
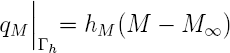
En plus du traitement particulier exigé par la condition de contact nous avons un problème lié aux conditions limites mécanique. Nous "manquons" de conditions aux bords, le problème est "mal posé" (au sens de Hadamard) puisque nous n'avons pas unicité de la solution. Le problème tel que proposé admet comme solution des translations dans une direction privilégiée d'une solution initiale (mouvements de corps rigide). Pour remédier à cette situation nous introduirons une modification à l'algorithme de résolution permettant d'exclure les mouvements de corps rigide. Notons que cette modification correspond à imposé qu'en tout temps au moins un point de la surface inférieure du panneau ait un déplacement nul. Ce qui correspond en fait à une condition limite du type:
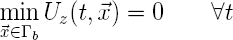
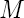 | teneur en humidité (kg kg-1 X 100) |
 | densité (kg m-3) |
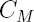 | constante valant 1/100 |
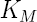 | tenseur de diffusion effective (kg m-1 s-1 %-1) |
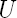 | vecteur des déplacements (m) |
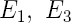 | module d'Young (Pa) |
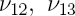 | coefficient de Poisson (m m-1) |
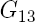 | coefficient de cisaillement (Pa) |
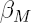 | tenseur de dilatation hydrique (%-1) |
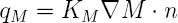 | flux d'humidité dans la direction normale n |
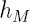 | coefficient de convection hydrique (kg m-2 s-1 %-1) |
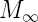 | La teneur en humidité ambiante |
Retour en haut


