Un autre élément important dans l'élaboration d'un code élément finis est le choix du solveur pour le système algébrique. MEF++ utilise pour la résolution la librairie PETSc (Portable, Extensible Toolkit for Scientific Computation ). Il est cependant possible d'utiliser d'autres outils, mais PETSc est la librairie intégrée à MEF++.

• SolveurLinPETSc est le solveur nécessaire pour un problème élément fini statique et linéaire. Cette classe permet de résoudre les systèmes linéaires de la forme:
  
  Cette classe permet de choisir une grande variétés de méthode de résolution (directes ou itératives) et un grand nombre de préconditionneur.
  
  
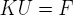
• SolveurNlinPETSc résout un système non-linéaire (provenant d'équations aux dérivées partielles non linéaire) de la forme
  
  en procédant par corrections successives (point fixe): à chaque itération on résout un système linéaire en utilisant un solveur de la classe SolveurLinPETSc.
  
  
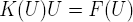
• SolveurInstNlinPETSc permet de résoudre des problèmes provenant de la semi-discrétisation d'une équation aux dérivées partielles d'ordre 1 en temps. Cette classe est conçue pour le cas le plus général possible. La forme du système discret est
  
  À chaque pas de temps on utilise un objet de la classe SolveurLinPETSc. Si le problème est non-linéaire on utilise une méthode de point fixe à chaque pas de temps. Pour le schéma en temps on a comme schémas: Euler explicite, Crank-Nicholson, Galerkin, Euler implicit, Theta et Gear.
  
  
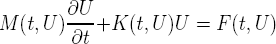
• SolveurInstO2NewmarkPETSc est la classe qui traite les problèmes provenant de la semi-discrétisation d'une équation aux dérivées partielles d'ordre 2 en temps (sans amortissement). Cette classe est conçue pour le cas le plus général possible tout en tenant compte de la limitation imposée. La forme du système discret est
  
  La méthode de Newmark est appliquée au système pour le résoudre. Ici aussi on utilise un objet de la classe SolveurLinPETSc à chaque pas de temps et on utilise une méthode de point fixe si le problème est non-linéaire.
  
  
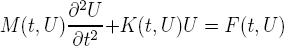
• SolveurGCP et SolveurGCPAvecCorpsRigide sont des classes particulières de solveur. Il s'agit de solveur permettant de résoudre des problèmes dont la forme discrète se ramène à un problème d'optimisation
  
  C'est la forme que prendra, entre autre, un problème de contact unilatéral en élasticité linéaire quasi-statique. L'optimisation se fait en utilisant la méthode de gradient conjugué projeté. La classe SolveurGCPAvecCorpsRigide nous fourni un solveur ayant la particularité de traiter les problèmes où les mouvements de corps rigides ne sont pas exclus (problèmes "mal posés").

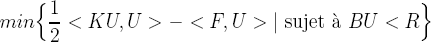
Retour en haut