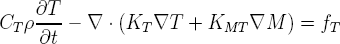
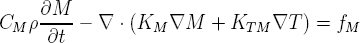
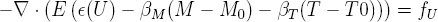
Couplages explicites

Les ÉDP à l'étude comportent des couplages explicites sous la forme de terme de formulation (par exemple le gradient de M apparaît dans l'équation décrivant T et vice-versa). Ce couplage évident fait en sorte que l'on doit résoudre simultanément les équation pour T et M. Notons que si l'on néglige l'effet de M sur T (K_MT = 0) ou de T sur M ( K_TM = 0) alors on pourra résoudre séparément mais en séquence les deux équations. Notons que pour les déplacements, a priori, on a pas de couplages avec la température et la teneur en humidité. On peut donc résoudre le système en U après la résolution du système en T-M.

Couplages explicites

Il faut noter un second type de couplages. Il s'agit de couplages implicites ayant deux origines: via les coefficients et différents paramètres servant à définir le comportement physiques des variables d'état: par exemple la dépendance des coefficients de diffusion K_M par rapport à T peut faire apparaître un couplage entre T et M même si K_TM = 0. On peut aussi faire apparaître des couplages via les conditions aux bords. Ainsi lors du séchage il est concevable d'imposer une condition de convection qui changera selon l'état des déplacements (variation du coefficient de convection dûe à la variation de l'exposition d'une face). Dans ce cas on a un couplage entre les 3 variables.

Conditions limites et problème de contact

Les processus que nous traitons comportent, pour la plupart d'entre eux, une phase de séchage ou exposition à l'humidité. Durant cette phase on a qu'une seule condition limite pour la composante mécanique. Le panneau (ou tout autre objet à l'étude) est en effet "posé" sur un support et la seule condition qui soit réaliste dans ce cas est d'imposer que le panneau ne "pénètre" pas le support sur lequel il est posé. Cette condition limite se traduit par une inégalité pour les déplacements. Il est possible dans certain cas d'introduire un artifice permettant de formuler cette condition via des conditions limites usuelles. Cependant nous nous intéressons plutôt à une formulation le plus près possible de la réalité, nous avons donc choisi de conserver cette inégalité comme condition limite. Cette condition nous donne alors pour l'élasticité un problème de contact.

Retour en haut