Felix Kwok Département de mathématiques et de statistique Université Laval

• Home
• Research
• Publications
• Books
• Teaching
• Links

• EN
• FR

Research interests

My general research interests revolve around algorithms and techniques for efficient large-scale simulations in physics and engineering, particularly when the models are described by PDEs or systems of PDEs. Typically, such simulations must repeatedly solve large, sparse linear and nonlinear systems of equations that result from discretizing the PDEs. To extract maximum efficiency, it is crucial to employ fast, robust and mathematically sound linear and nonlinear solvers, specialized to exploit both the underlying physics of the problem and well-known numerical techniques. Solver design is thus a fascinating topic that lies at the crossroads of mathematical analysis, scientific computing and engineering. It is this fundamentally interdisciplinary nature that I find particularly stimulating and rewarding.

Current projects

Domain Decomposition Methods

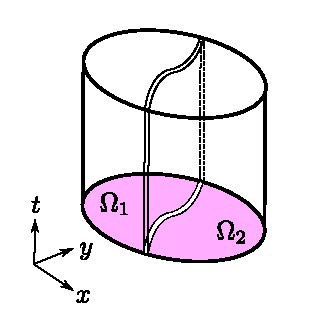
In domain decomposition methods, the computational domain is divided into several subdomains, and the subdomain equations are solved in parallel. An iteration is then performed to ensure the solutions are consistent across subdomain boundaries. The convergence rate of this iteration is highly dependent on the nature of the PDE and on the precise boundary conditions used along subdomain boundaries. Several problems I have been working on include:
Waveform relaxation methods for time-dependent PDEs. Instead of discretizing first in time and solving the resulting sequence of spatial PDE by domain decomposition, one can first decompose in space and consider each subdomain problem as a space-time problem and solve them independently. This approach, known as waveform relaxation, yields additional flexibility in the choice of spatial and temporal grids and allows the use of black-box solvers for subdomain problems. We are interested in the effect of different transmission conditions, as well as how to incorporate a coarse grid correction to obtain convergence that is nearly independent of the number of subdomains.
Time-domain decomposition for optimization problems with PDE constraints. Optimization problems with PDE constraints arise in many applications, such as enhanced oil recovery, contaminant tracking and biomedical applications. In addition to the governing PDE and initial conditions, optimization problems satisfy an adjoint PDE, which runs backward in time from a final condition and is coupled with the original forward PDE. To solve this two-point boundary value problem (initial and final time), the time horizon can be divided into several time windows, and each time window can be solved in parallel. For parabolic control problems, we have shown that an appropriate choice of optimized transmission conditions leads to a method that converges for any number of subdomains, with a rate of convergence that is independent of the mesh size used in each subdomain.
Algebraic derivation of optimal transmission conditions. We have shown that for a large class of linear PDE boundary value problems, there is a suitable (nonlocal) transmisison operator for which the associated domain decomposition iteration converges in a finite number of steps, regardless of how the subdomains are interconnected. Ongoing work focuses on the local approximation of such operators and how they affect the asymptotic convergence rate under grid refinement. Slides on optimal interface conditions, presented at the 19th Domain Decomposition Conference in Zhangjiajie, China (PDF, 397kb)

Fast solvers for reservoir simulation

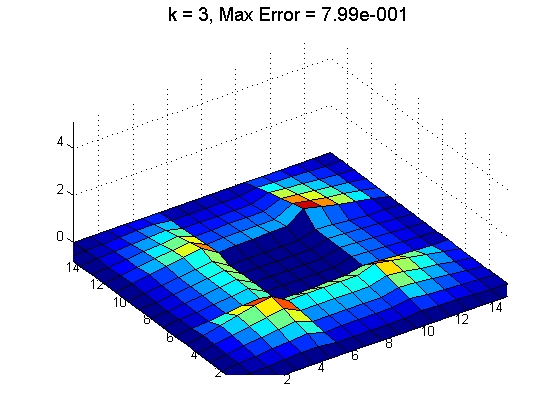
The reservoir equations, though highly nonlinear, are directional in nature because it models fluid flow in a porous medium. Linear and nonlinear solvers can exploit this directionality to obtain a partial decoupling of the unknowns and solve them sequentially. The resulting Newton-based nonlinear solver becomes more robust with respect to time-step sizes. Meanwhile, the linear solver also converges more quickly and becomes less sensitive to flow configurations. Ongoing research seeks to quantify these benefits and to extend the methodology to other problems that are directional in nature, such as Navier-Stokes. Slides on ordering methods in reservoir simulation (PDF, 1.6Mb)

Fully-Implicit Method 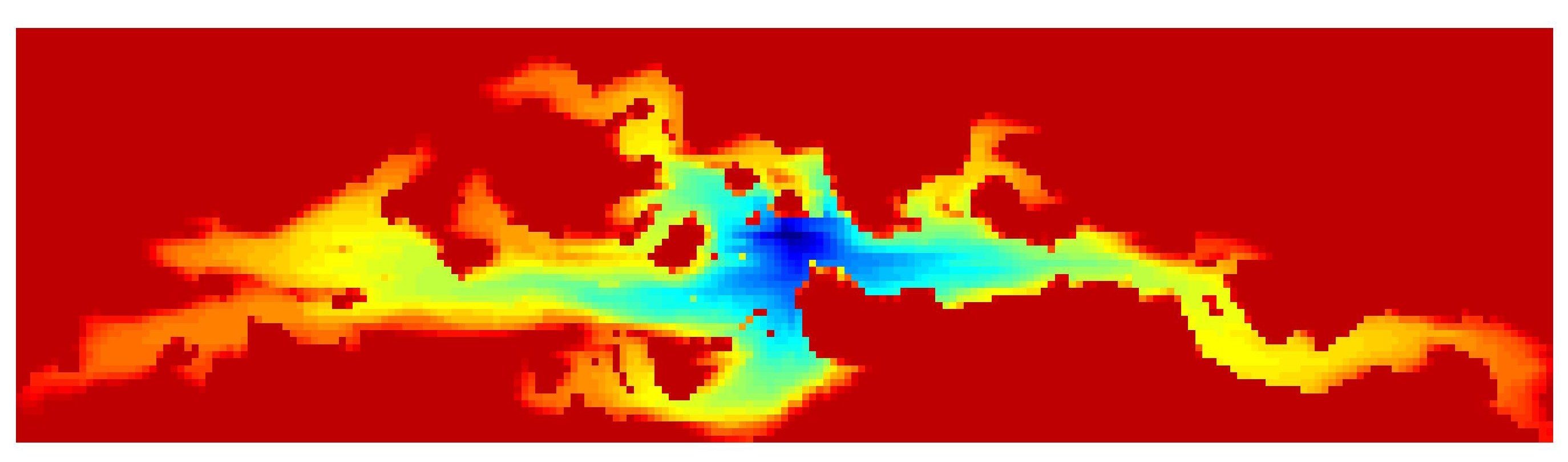Implicit Pressure/Explicit Saturation