Felix Kwok
Département de mathématiques et de statistique
Université Laval

Programme de recherche

Mon programme de recherche porte généralement sur la conception des méthodes numériques pour des simulations à haute résolution en physique et en génie. Dans de telles simulations, le phénomène physique est souvent modélisé par des équations aux dérivées partielles (EDP), et le but est de suivre l'évolution du système en résolvant approximativement ces EDP à plusieurs points en espace et en temps. Ceci nécessite la résolution à plusieurs reprises des systèmes d'équations linéaires et non linéaires de tailles énormes, comportant souvent des millions de degrés de liberté. Il est donc primordial de développer des algorithmes de résolution (des "solveurs") efficaces, et de les analyser mathématiquement afin de comprendre leurs comportements par rapport aux paramètres physiques du problème. La conception des solveurs efficaces est donc un sujet passionnant qui touche à plusieurs branches de mathématiques, telles que l'analyse fonctionnelle, le calcul scientifique et la modélisation mathématique, et qui ont des applications intéressantes en physique, génie et biologie.

Projets récents

Décomposition de domaine

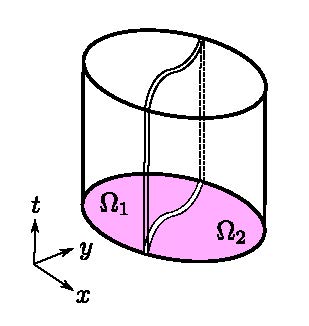
Dans une méthode de décomposition de domaine (DD), le domaine de calcul est subdivisé en plusieurs sous-domaines. En imposant l'EDP sur ces sous-domaines plus petits, on obtient des sous-problèmes avec moins de degrés de liberté qui peuvent être résolus indépendamment les uns des autres. Les méthodes DD sont donc parfaitement adaptées aux grappes de calcul avec des milliers de coeurs, puisque chaque sous-domaine peut être traité par un coeur différent, et cela de façon parallèle; on peut ainsi réduire dramatiquement le temps de calcul pour des problèmes complexes. Pour retrouver la solution du problème de départ, il faut imposer des équations supplémentaires pour assurer la continuité de la solution à travers des interfaces entre sous-domaines. Ces équations sont résolues à l'aide des méthodes itératives. La vitesse de convergence de ces dernières dépend très fortement de l'EDP en question ainsi que du choix de conditions d'interface. Une analyse de convergence pour certains problèmes modèles est donc indispensable si on veut développer des algorithmes performants et robustes pour des problèmes plus réalistes. Voici quelques sujets que j'ai traités récemment :

  • Méthodes de relaxation d'ondes pour des problèmes instationnaires. La plupart des méthodes DD classiques sont conçues pour des problèmes stationnaires. Pour des problèmes évolutifs, l'approche standard consiste à discrétiser d'abord en temps pour obtenir une suite de problèmes stationnaires; ces problèmes sont alors résolus l'un après l'autre par des méthodes DD. Les méthodes de relaxation d'ondes (waveform relaxation, WR), quant à elles, définissent des problèmes en espace-temps dans chaque sous-domaine; une itération convergente assure alors la continuité de la solution à travers des interfaces partout dans l'intervalle de temps concerné.

    L'approche WR permet de choisir sur chaque sous-domaine une discrétisation différente en espace-temps, afin de mieux s'adapter aux variations locales de la solution. Elle permet aussi de résoudre des problèmes multiphysiques où chaque sous-domaine est gouverné par un modèle différent : s'il existe déjà des solveurs efficaces pour chaque modèle, il suffit de les combiner avec une méthode itérative appropriée pour satisfaire les conditions de continuité entre sous-domaines. Ici, la question pertinente consiste à analyser la vitesse de convergence des méthodes WR en fonction des conditions d'interface imposées. De plus, pour des décompositions avec un grand nombre de sous-domaines, il est important de bien choisir la stratégie de communication globale (à l'aide d'une grille grossière, par exemple), afin de maintenir une vitesse de convergence adéquate, quel que soit le nombre de sous-domaines.
  • Décomposition de domaine en temps pour des problèmes d'optimisation. Des problèmes d'optimisation soumise à des contraintes de type EDP se manifestent naturellement dans plusieurs applications, telles que l'exploitation des réserves pétrolières, le suivi des contaminants et des applications biomédicales. Lorsque l'EDP issue du modèle physique est instationnaire, le système d'optimalité comprend non seulement cette EDP, mais aussi une EDP adjointe qui évolue dans le sens opposé dans le temps, c.-à-d., de l'état final vers l'état initial. Pour résoudre ce système couplé d'EDP, on découpe l'intervalle de temps en plusieurs sous-intervalles, afin d'obtenir des problèmes de tailles réduites qu'on peut résoudre en parallèle. Pour le contrôle parabolique, il existe un choix de conditions d'interfaces qui donne une méthode convergente pour un nombre arbitraire de sous-intervalles, et dont le taux de convergence est indépendant du maillage utilisé dans chaque sous-intervalle.
  • Dérivation algébrique des conditions d'interface optimales. Pour une classe assez large d'EDP elliptique, on peut définir des opérateurs de transmission non locaux ainsi que des méthodes DD employant ces opérateurs, de façon à ce que la méthode converge vers la solution exacte dans un nombre fini d'itérations. L'existence de ces opérateurs ne nécessite aucune hypothèse sur la connectivité des sous-domaines. Or, ces opérateurs non locaux sont difficiles à implémenter; l'objectif actuel est de trouver de bonnes approximations locales pour ces opérateurs et d'étudier le taux de convergence des méthodes DD qui utilisent ces approximations, en fonction de la taille du maillage dans chaque sous-domaine.

Solveurs spécialisés pour des écoulements en milieux poreux

Les équations modélisant l'écoulement de fluides en milieux poreux sont fortement non linéaires et posent souvent des difficultés aux solveurs linéaires et non linéaires lors des simulations. Malgré ces difficultés, il est possible d'exploiter le caractère directionnel de ces écoulements pour découpler partiellement ces systèmes d'équations non linéaires. En appliquant la méthode de Newton à ces systèmes partiellement découplés, on obtient un solveur plus robuste par rapport aux pas de temps utilisés dans la simulation. De plus, on observe une convergence plus rapide du solveur linéaire suite à un tel découplage, car il réduit l'influence de l'orientation de l'écoulement sur la matrice jacobienne. Il reste à quantifier plus précisément ces avantages et à étendre cette approche aux autres équations avec un caractère directionnel, telles que celles de Navier-Stokes. Fully-Implicit Method
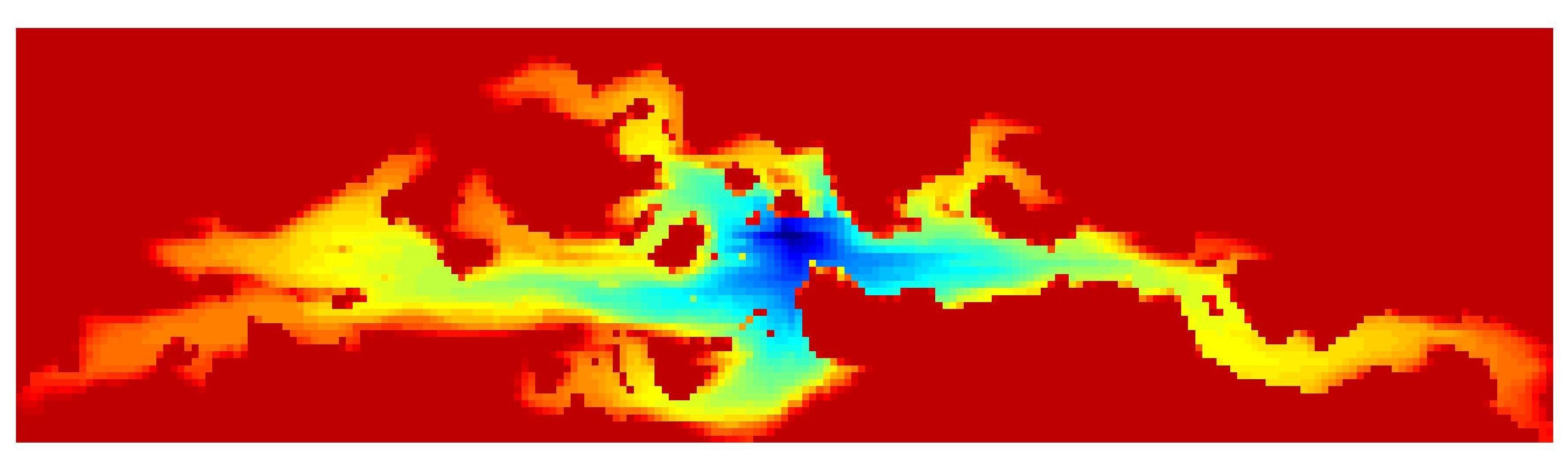Implicit Pressure/Explicit Saturation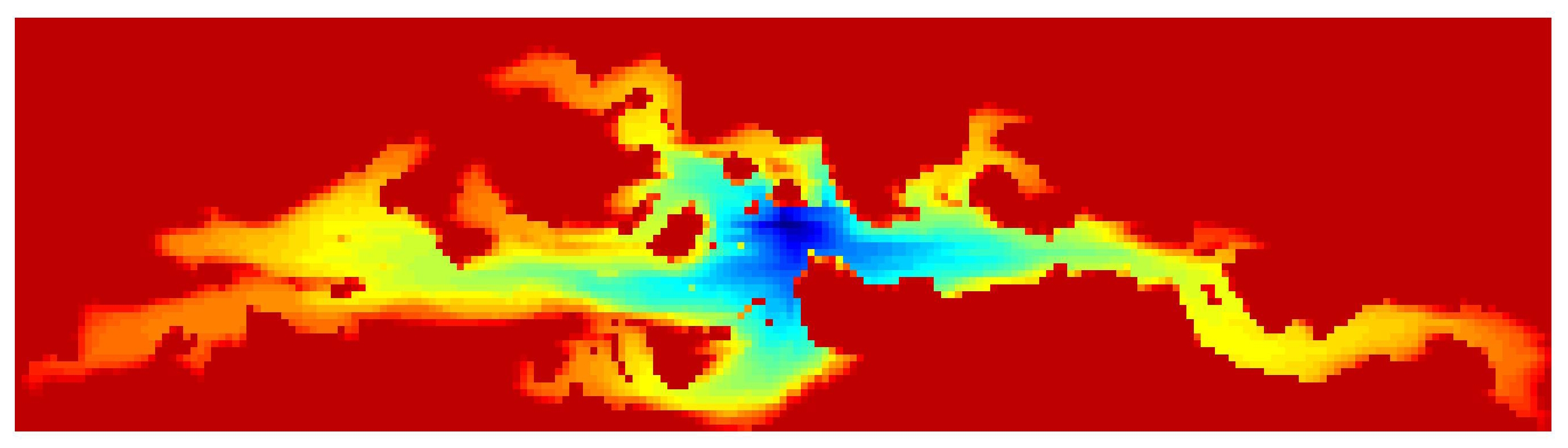